En 1900, en faisant des analyses sur le rayonnement thermique émis par des corps noirs, Max Planck découvrit qu’il y a une relation directe entre l’énergie d’un rayonnement thermique et la fréquence (longueur d’onde) de ce rayonnement. En fait, il réalisa que plus la fréquence du rayonnement est élevée, plus l’énergie est grande. Il conclut donc que l’énergie d’un rayonnement thermique est directement proportionnelle à la fréquence du rayonnement multipliée par une constante qu’il a défini durant ces analyses. Ce calcul lui permettait d’obtenir une bonne évaluation de l’énergie contenue dans chaque rayonnement en particulier. La fameuse équation Energie d’un photon (E) = Constante de Planck multipliée par la Fréquence du rayonnement vient des résultats de ces travaux de Max Planck, et la fameuse constante utilisée par Planck devint la « Constante de Planck ».
En 1839, Antoine Becquerel et son fils Alexandre Edmond avaient abordé pour la première fois un phénomène photoélectrique. Ils démontrèrent, en effet, qu’en modifiant l’éclairage sur des électrodes, la résistivité de celles-ci changeait. En fait, plus les électrodes étaient éclairées, moins la résistance était grande, et plus la quantité de courant qui les traversait augmentait. Ils en conclurent donc que la lumière influençait le déplacement des électrons dans les conducteurs sans toutefois pouvoir expliquer ce phénomène.
C’est Heinrich Rudolf Hertz qui expliqua pour la première fois les causes physiques de ce phénomène. Il publia ses résultats dans la revue scientifique Annelen der Physik en 1887. Cependant, on dut attendre jusqu’en 1905 avant que ces phénomènes puissent être quantifiés par des explications scientifiques et par des équations.
Ce n’est nul autre qu’Albert Einstein qui émit la théorie physique expliquant ce phénomène. Einstein expliqua que ce phénomène était provoqué par l’absorption de l’énergie de l’onde lumineuse qui frappait le matériau. Il fut le premier à définir la lumière comme étant des quantas de lumière qu’on appelle aujourd’hui « Photons ». Cette explication lui valut le prix Nobel de Physique en 1921. Pour expliquer le phénomène, il utilisa la relation développée par Planck quelques années auparavant, à savoir que l’énergie d’un quanta de lumière était égale à la Constante de Planck multipliée par la fréquence de cette onde lumineuse. Einstein émit aussi l’hypothèse qu’une onde lumineuse transmettait son énergie au matériau quand celui-ci y était exposé. Si l’énergie du photon était suffisamment grande, celui-ci réussissait à extraire un électron de la matière et cet électron était projeté dans l’espace. Einstein définit une équation qui montre que l’énergie cinétique acquise par l’électron dans l’espace est en fait la différence entre l’énergie initiale du photon et l’énergie requise pour extraire l’électron de la matière. Par exemple, si on expose un matériau à un quanta de lumière dont les photons ont une énergie de 2,12 électronvolts (les électronvolts sont les unités de mesure utilisées pour définir l’énergie d’un photon), et que l’énergie nécessaire pour extraire un électron du matériau est de 1,48 électronvolts (eV), l’électron frappé par ce photon acquerra 0,64 eV d’énergie, soit 2,12 – 1,48 = 0,64 eV. C’est cette énergie qui permettra à l’électron de s’extraire du matériau. L’énergie d’extraction sera égale à la masse de l’électron multipliée par sa vitesse au carré, divisée par 2 (E = m*v^2/2). C’est grâce à cette énergie excédentaire qu’on peut faire circuler un courant dans une lampe photoélectrique. Dès qu’un photon frappe l’écran de la lampe avec une énergie supérieure à l’énergie d’extraction du matériau de l’écran de la lampe, des électrons sont émis vers l’anode.
En 1913, Niels Bohr propose un modèle intéressant pour comprendre la façon dont les photons sont générés. Le modèle de Bohr suggère que les électrons attachés au noyau d’un atome ne peuvent occuper que certains niveaux spécifiques. Comme illustré dans le graphique ci-joint pour l’atome d’hydrogène où les niveaux d’énergie permis sont illustrés.
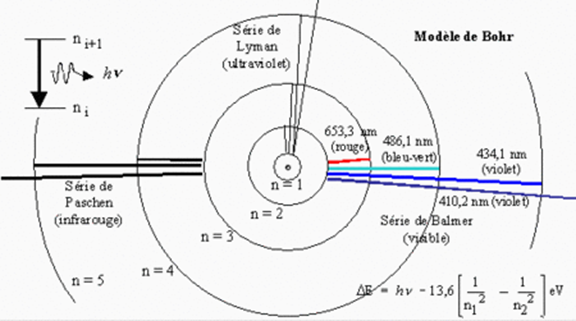
Les niveaux d’énergies et les séries de raies de l’atome de Bohr. © Guy Collin, professeur émérite, UQAC
Bohr propose aussi que chacun des niveaux permis soit associé à un niveau d’énergie. Ce modèle permet d’illustrer que de l’énergie est requise ou émise lors d’un passage d’un électron d’un niveau à un autre. Il avança aussi l’hypothèse qu’un photon pouvait fournir l’énergie requise pour passer d’un niveau à un autre et qu’un photon pouvait être émis lorsqu’un électron passe d’un niveau plus élevé à un niveau inférieur. Ainsi, dans l’atome d’hydrogène, pour faire passer un électron d’un niveau 2 à un niveau 3, il faudra lui fournir une énergie équivalente à un photon de couleur rouge.
La société scientifique moderne accepte le fait que l’émission d’un photon résulte du passage d’un électron d’un niveau à un autre. Ainsi, dès qu’un matériau est frappé par un photon, ce photon est absorbé par le matériau et un électron est déplacé d’un niveau à un autre. Si l’énergie contenue dans le photon est supérieure à l’énergie requise pour faire passer cet électron d’un niveau jusqu’au dernier niveau d’énergie de l’atome, on comprendra que l’électron sera éjecté du matériau. On appelle ce phénomène ionisation. C’est ce phénomène qu’Einstein a illustré en 1905. En fait, c’est de cette façon que les phénomènes photoélectriques sont générés.
C’est en se basant sur ce phénomène que l’industrie a développé des lampes photoélectriques. Une lampe photoélectrique est constituée d’un écran qui peut capter des photons. Lorsqu’un photon atteint l’écran (Cathode) d’une lampe photoélectrique, un électron est émis. Si on établit une différence de potentiel favorable entre la cathode et l’anode d’une lampe photoélectrique, l’électron extrait de la cathode sera attiré par l’anode et s’y déposera.
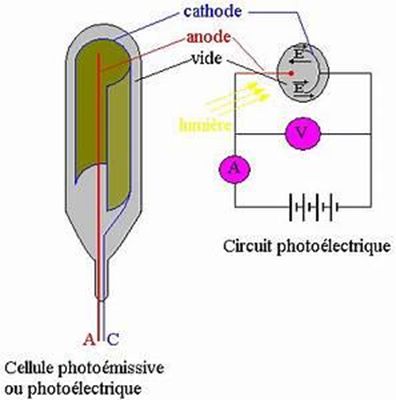
Chaque photon a donc une énergie qui lui est propre. Plus la fréquence de ce photon est grande, plus son énergie sera grande. Dès lors pour faire sauter un électron de la cathode vers l’anode, le photon devra avoir un minimum d’énergie. Par exemple, on peut trouver sur le marché des lampes photoélectriques qui émettront des électrons si elles sont frappées par des photons ayant des longueurs d’onde (une longueur d onde, c’est 1/ fréquence de cette onde) variant de 400 à 700 nanomètres. Comme un photon de 400 nanomètres a beaucoup plus d’énergie qu’un photon de 700 nanomètres, il faudra plus d’énergie pour arrêter son passage de la Cathode à l’Anode.
On a utilisé cette caractéristique pour valider la valeur de la constante de Planck. En effet, chaque photon de fréquence différente projeté sur la Cathode d’une lampe photoélectrique nécessitera la génération d’un potentiel d’arrêt différent. C’est-à-dire qu’il faudra lui opposer une force équivalente à l’énergie excédentaire détenue par ce photon. En répétant cette opération à plusieurs reprises pour des photons de fréquences différentes, on peut obtenir une série de potentiel d’arrêt pour une série de photons correspondants. Si on trace un graphique à l’aide de ces résultats en mettant les potentiels d’arrêt sur l’axe des Y et la fréquence du photon projeté sur la Cathode sur l’axe des X, on pourra tracer une droite dont la pente s’avérera être égale à la constante de Planck. C’est d’ailleurs de cette façon qu’on peut aujourd’hui encore estimer l’ordre de grandeur de la constante de Planck. Or, ce type d’expérience prend pour acquis que peu importe la source lumineuse qui génèrera les ondes de 400 à 700 nanomètres, les résultats seront toujours les mêmes puisque l’énergie des photons générés sera la même pour tous les photons ayant les mêmes fréquences. En effet, l’équation qui définit l’énergie d’un photon est E = h*f. Comme constat dans cette équation, il n’y a que la fréquence qui peut varier puisque la constante de Planck (h) est une constante qui ne varie pas. Il n’y a que deux paramètres dans l’équation : une constante et la fréquence du photon. Ainsi selon cette équation, un photon ayant une fréquence équivalente à une longueur d’onde de 590 nanomètres aura toujours la même énergie indifféremment de la source lumineuse qui générera ce photon. Donc, toutes les ondes lumineuses de 590 nanomètres générées dans l’univers sont réputées avoir exactement la même énergie et nécessiteront le même potentiel d’arrêt afin de réduire le courant à zéro dans une lampe photoélectrique.
Afin de vérifier la véracité de ce dernier énoncé, l’équipe de chercheurs d’Opsun Technologies Inc a effectué la série d’expériences décrites ci-après. Le but de ces expériences menées était de vérifier si le potentiel d’arrêt serait le même pour toutes les ondes lumineuses de 590 nanomètres peu importe la source qui les génère. On se rappelle que selon la théorie, le potentiel d’arrêt d’une onde lumineuse de 590 nanomètres devrait être le même peu importe la source qui a généré cette onde lumineuse. Le montage suivant a donc été réalisé : Une lampe photoélectrique ayant une bonne sensibilité à des photons de 590 nanomètres a été installée à l’intérieur d’une boîte noire. Devant cette lampe, un filtre de précision optique de 590 nanomètres a été installé de façon à s’assurer qu’il n’y aurait que les photons de 590 nanomètres qui pourraient se rendre jusqu’à la lampe photoélectrique. Puis, une lentille a été placée devant le filtre et un obturateur a été ajouté de façon à pouvoir ajuster le diamètre du faisceau lumineux, et à concentrer le faisceau lumineux sur le filtre.
Dans les expériences initiales, la puissance du faisceau lumineux qui était projeté sur l’écran de la lampe photoélectrique n’avait pas été mesurée avec précision, aucune cache n’avait été installée sur la lampe photoélectrique et le niveau de précision des instruments de mesure utilisés par Opsun était nettement insuffisant. En effet, nous avons réalisé que la puissance du faisceau qui atteignait l’écran de la lampe ainsi que son diamètre étaient susceptibles d’influencer les potentiels d’arrêt. De la même façon, lorsque le potentiel d’arrêt arrive très près de son niveau zéro courant, les courants de la lampe photoélectrique sont de l’ordre de 0,0001 milliampère, soit 100 nano ampères. Sans l’utilisation d’un instrument de mesure de précision, il devient très difficile d’identifier le potentiel d’arrêt exactement au niveau ou le courant est vraiment à zéro. Afin de pallier aux erreurs que ces trois éléments ont pu occasionner, l’équipe d’Opsun a décidé de recommencer une nouvelle série de tests dans un laboratoire d’optique spécialisé. Cette nouvelle série d’expériences a été réalisée dans le laboratoire du COPL de l’Université Laval à Québec en février 2022.
Pour réaliser cette nouvelle série d’expériences, cinq nouvelles sources lumineuses ont été utilisées. L’une de ces sources était de type tungstène, deux étaient de type à LED, une autre était de type laser et la dernière était une lampe au sodium. Une mesure au spectromètre a été effectuée pour chaque source afin de s’assurer que chacune de ces lampes générait bien des photons à 590 nanomètres à la sortie du filtre en quantité suffisante. La puissance du faisceau lumineux a aussi été ajustée ainsi que son diamètre. Chacun des tests avec chacune des lampes a été effectué en utilisant la même méthodologie. Le potentiel d’arrêt a été généré par une source DC de haute précision modèle ‘’source meter 2400 de Keithley ‘’pouvant mesurer des pico ampères. Cet appareil peut générer des tensions et les mesurer, tout en mesurant le courant de l’ordre des pico ampères qui circulait dans la lampe photovoltaïque. Une fois la source lumineuse allumée, une vérification était faite afin de s’assurer que le faisceau lumineux illuminait la lampe en remplissant parfaitement bien la cache circulaire installée sur la lampe photoélectrique. La puissance du faisceau lumineux était mesurée, et ajusté au niveau de 100 micro watts par cm^2. Ensuite, la tension du potentiel d’arrêt était augmentée par tranche de 50 millivolts, et une mesure du courant qui circulait dans la lampe était faite avec précision. La tension du potentiel d’arrêt était augmentée au fur et à mesure jusqu’à ce que le courant émis par la lampe photoélectrique tombe à zéro. A ce point, la tension requise comme potentiel d’arrêt était notée pour cette source lumineuse. La même procédure a été répétée pour chacune des sources lumineuses.
Que nous apprennent ces nouvelles expériences ?
On se rappèle que selon la théorie actuelle, le potentiel d’arrêt mesuré pour chacune des cinq sources lumineuses aurait dû être le même puisque les photons émis avaient tous une longueur d’onde identique de 590 nanomètres, donc la même fréquence. Or les mesures effectuées par l’équipe d’Opsun n’ont pas permis de valider cette hypothèse. En effet, en utilisant des sources lumineuses différentes qui génèrent pourtant toutes des photons ayant des longueurs d’onde de 590 nanomètres, Opsun a constaté que les potentiels d’arret étaient sensiblement différents d’une source lumineuse à l’autre. Pour la petite lampe LED, le potentiel d’arrêt mesuré a été de 690 millivolts, celui de la lampe sodium a été de 660 millivolts , celui du crayon laser de 589 nm a été de 590 millivolts , celui de la grosse lampe LED a été de 550 millivolts, et celui de la lampe tungstène a été de 540 millivolts . Alors qu’on s’attendait à observer des potentiels d’arrêt identiques, voici que ces potentiels d’arrêt varient de plus de 150 millivolts. La seule explication possible à ces résultats, c’est que l’énergie de chacun de ces photons de 590 nanomètres n’est pas la même. Les photons de la petite lampe LED seraient les plus énergétiques tandis que ceux de la lampe au tungstène seraient ceux qui ont le moins d’énergie. A la lumière de ces résultats, nous devons conclure que l’équation définissant l’énergie d’un photon qui est une multiplication de la constante de Planck par la fréquence de l’onde lumineuse ne constitue pas une juste représentation de la véritable énergie d’un photon. Ces résultats mettent en évidence que l’énergie d’un photon ne peut pas être évaluée en utilisant une constante de Planck universelle.
Nous émettons ici notre première hypothèse à l’effet que la constante de Planck n’est pas universelle, mais bien relative à la source lumineuse qui génère les photons.
L UNIVERS DES ONDES OSCILLANTES
Dans l’univers des ondes oscillantes, c’est l’amplitude qui détermine la différence d’énergie entre deux ondes vibrant à la même fréquence. Ainsi, par exemple, on contrôle la puissance d’un faisceau laser en faisant varier l’amplitude de l’onde lumineuse qu’il génère. Plus l’amplitude est grande, plus la puissance du faisceau est grande à la même fréquence.
Un dispositif constitué d’un ressort ayant un coefficient de rappel K ancré au plafond au bout duquel un poids de masse M a été fixé nous permet de bien visualiser ce phénomène. La fréquence d’oscillation de ce dispositif est unique. Elle est uniquement reliée à la combinaison du coefficient de rappel du ressort K et de la masse M du poids qui y est attaché. Ce dispositif oscillera à une fréquence égale à la racine carré de la division du coefficient de rappel par la masse du poids M . (( K/M ) ^ 0,5 ). Ce dispositif ne pourra pas osciller à une autre fréquence que celle-ci. Cependant, on pourra faire varier à volonté l’énergie d’un tel dispositif en faisant simplement varier l’amplitude du déplacement, de l’oscillation. On pourra facilement vérifier que l’énergie de ce dispositif étiré de 10 cm sera quatre fois grand que celle du même dispositif étiré de 5 cm, puisque l’énergie de ce dispositif sera égale au coefficient de rappel (K) multiplié par l’amplitude au carré, le tout divisé par 2 ( K * A^2 ) / 2 . Notons que dans les deux cas, la fréquence d’oscillation sera la même.
Nous émettons donc ici notre deuxième l’hypothèse à l’effet que les photons sont aussi dotés d’une amplitude et qu’il existe des ondes lumineuses ayant des énergies différentes à la même fréquence parce que leur amplitude est différente.
Lors de cette série d’expériences, Opsun a aussi mesuré les potentiels d’arrêt de deux faisceaux laser en interférence. A l’aide d’un interféromètre de Michelson, chacun des faisceaux laser ont été projetés séparément sur la lampe photovoltaïque sans interférence dans un premier temps, puis sans modifier rien d’autre, dans un état d’interférence en déplacement seulement légèrement l’un des miroirs de l’interféromètre. Dans les deux cas, les potentiels d’arrêt des faisceaux lumineux ont montré un potentiel d’arrêt beaucoup plus élevé lorsqu’ils étaient en interférence. Ces résultats démontrent une fois de plus que l’énergie d’un photon ne peut pas être déterminée exclusivement par la multiplication de la constante de Planck par la fréquence du photon. Pour déterminer correctement l’énergie d’un photon, on doit développer une formule qui inclura l’amplitude comme variable importante.
Travaux de recherche effectués par Raymond Gilbert
12 Juin 2020


